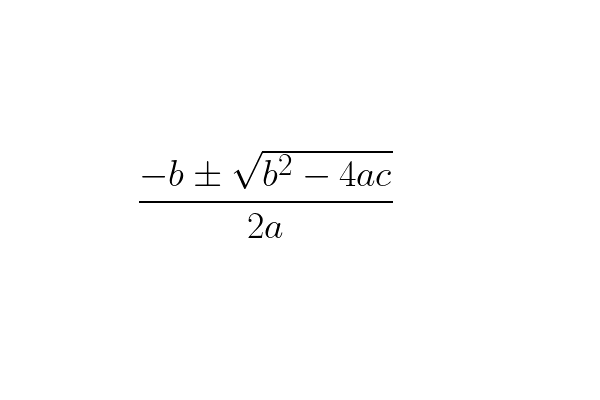Programs to find the roots of a quadratic equation have been shown here. The standard form of a quadratic equation is $ax^2+bx+c = 0$ where $x$ is the unknown and $a, b, c$ are the coefficients. The roots can be either imaginary or real depending on the value of discriminant $b^2 - 4ac$.
Page content(s):
1. Algorithm to find the roots of a quadratic equation
1. Take the values of $a, b, c$ as inputs.
2. Compute discriminant $d= b^2 - 4ac$.
3. If $d$ is negaive, display $\frac{-b+ \sqrt{-(b^2 - 4ac)}}{2a}$ and $\frac{-b- \sqrt{-(b^2 - 4ac)}}{2a}$ as the roots.
4. If $d = 0$, display $\frac{-b}{2a}$ and $\frac{-b}{2a}$ as the roots.
5. If $d$ is positive, display $\frac{-b+ \sqrt{b^2 - 4ac}}{2a}$ and $\frac{-b- \sqrt{b^2 - 4ac}}{2a}$ as the roots.
2. Pseudocode to find the roots of a quadratic equation
Input : Values of $a, b, c$
Output :Roots of the quadratic equation $ax^2+bx+c = 0$
1. Procedure findRoots($a$, $b$, $c$):
2.
3.
4.
5.
6.
7.
8.
9. End Procedure
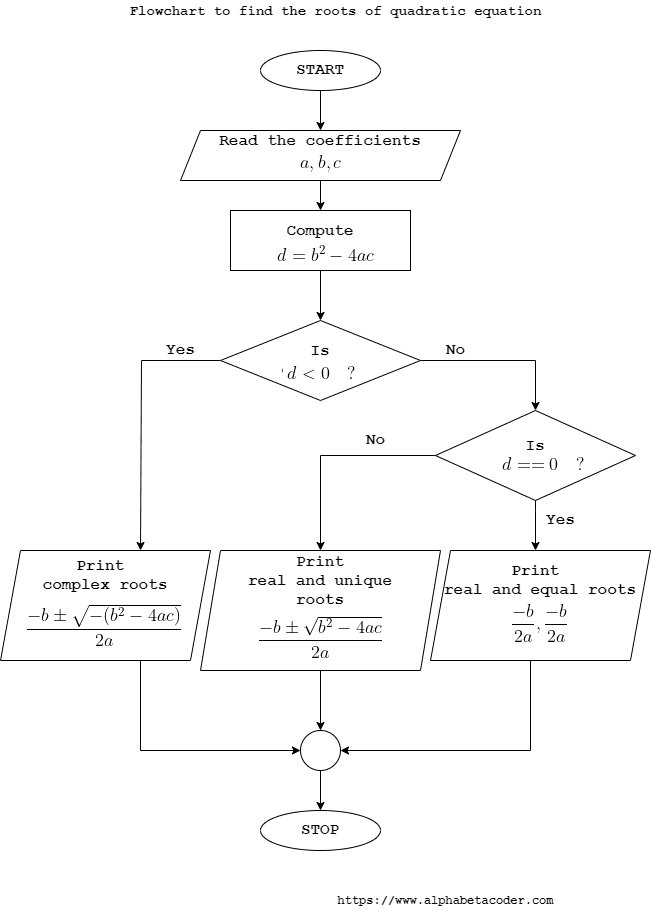
3. Flowchart to find the roots of a quadratic equation
4. Program & output to find the roots of a quadratic equation
This section covers the C, C++, Java, Python and C# programs to find the roots of a quadratic equation. The programs take the values of the coefficients $a, b, c$ as inputs to find the roots. The roots can either be complex or real and equal or real and unique.
4.1. C Program & output to find the roots of a quadratic equation
/************************************************** alphabetacoder.com C program to find the roots of quadratic equation **************************************************/ #include<stdio.h> #include<math.h> int main() { // delclare variables float a, b, c, d, r1, r2, im; // take input of a, b, c // for quadratic equation // ax^2 + bx + c = 0 printf("Quadratic equation ax^2 + bx + c = 0\n"); printf("Enter value of a: "); scanf("%f", & a); printf("Enter value of b: "); scanf("%f", & b); printf("Enter value of c: "); scanf("%f", & c); // calculate the value of discriminant b^2 - 4ac d = b * b - 4 * a * c; // if d < 0, the roots are complex // if d = 0, the roots are real and equal // if d > 0, the roots are real and distinct if (d < 0) { printf("The roots are complex.\n"); // calculate real part r1 = (-b) / (2 * a); // calculate imaginary part im = sqrt(d * -1) / (2 * a); // display roots printf("Root 1: %f + %fi\n", r1, im); printf("Root 2: %f - %fi\n", r1, im); } else if (d == 0) { printf("The roots are real and equal.\n"); // calculate the root r1 = (-b) / (2 * a); // display roots printf("Root 1: %f\n", r1); printf("Root 2: %f\n", r1); } else if (d > 0) { printf("The roots are real and unique.\n"); // calculate the roots r1 = ((-b) + sqrt(b * b - 4 * a * c)) / (2 * a); r2 = ((-b) - sqrt(b * b - 4 * a * c)) / (2 * a); // display roots printf("Root 1: %f\n", r1); printf("Root 2: %f\n", r2); } return 0; }
Output
Case 1:
Quadratic equation ax^2 + bx + c = 0
Enter value of a: 1
Enter value of b: -1
Enter value of c: 2
The roots are complex.
Root 1: 0.500000 + 1.322876i
Root 2: 0.500000 - 1.322876i
Case 2:
Quadratic equation ax^2 + bx + c = 0
Enter value of a: 1
Enter value of b: -4
Enter value of c: 4
The roots are real and equal.
Root 1: 2.000000
Root 2: 2.000000
Case 3:
Quadratic equation ax^2 + bx + c = 0
Enter value of a: 1
Enter value of b: -5
Enter value of c: 6
The roots are real and unique.
Root 1: 3.000000
Root 2: 2.000000
4.2. C++ Program & output to find the roots of a quadratic equation
/*************************************************** alphabetacoder.com C++ program to find the roots of quadratic equation ****************************************************/ #include<iostream> #include<cmath> using namespace std; int main() { // delclare variables float a, b, c, d, r1, r2, im; // take input of a, b, c // for quadratic equation // ax^2 + bx + c = 0 cout << "Quadratic equation ax^2 + bx + c = 0\n"; cout << "Enter value of a: "; cin >> a; cout << "Enter value of b: "; cin >> b; cout << "Enter value of c: "; cin >> c; // calculate the value of discriminant b^2 - 4ac d = b * b - 4 * a * c; // if d < 0, the roots are complex // if d = 0, the roots are real and equal // if d > 0, the roots are real and distinct if (d < 0) { cout << "The roots are complex.\n"; // calculate real part r1 = (-b) / (2 * a); // calculate imaginary part im = sqrt(d * -1) / (2 * a); // display roots cout << "Root 1: " << r1 << " + " << im << "i\n"; cout << "Root 2: " << r1 << " - " << im << "i\n"; } else if (d == 0) { cout << "The roots are real and equal.\n"; // calculate the root r1 = (-b) / (2 * a); // display roots cout << "Root 1: " << r1 << endl; cout << "Root 2: " << r1 << endl; } else if (d > 0) { cout << "The roots are real and unique.\n"; // calculate the roots r1 = ((-b) + sqrt(b * b - 4 * a * c)) / (2 * a); r2 = ((-b) - sqrt(b * b - 4 * a * c)) / (2 * a); // display roots cout << "Root 1: " << r1 << endl; cout << "Root 2: " << r2 << endl; } return 0; }
Output
Case 1:
Quadratic equation ax^2 + bx + c = 0
Enter value of a: 3
Enter value of b: 5
Enter value of c: 8
The roots are complex.
Root 1: -0.833333 + 1.40436i
Root 2: -0.833333 - 1.40436i
Case 2:
Quadratic equation ax^2 + bx + c = 0
Enter value of a: 1
Enter value of b: -10
Enter value of c: 25
The roots are real and equal.
Root 1: 5
Root 2: 5
Case 3:
Quadratic equation ax^2 + bx + c = 0
Enter value of a: 3
Enter value of b: 8
Enter value of c: -2
The roots are real and unique.
Root 1: 0.230139
Root 2: -2.89681
4.3. Java Program & output to find the roots of a quadratic equation
/*************************************************** alphabetacoder.com Java program to find the roots of quadratic equation ****************************************************/ import java.util.Scanner; public class Main { public static void main(String args[]) { // delclare variables double a, b, c, d, r1, r2, im; // declare an instance of scanner class Scanner sc = new Scanner(System.in); // take input of a, b, c // for quadratic equation // ax^2 + bx + c = 0 System.out.print("Quadratic equation ax^2 + bx + c = 0\n"); System.out.print("Enter value of a: "); a = sc.nextDouble(); System.out.print("Enter value of b: "); b = sc.nextDouble(); System.out.print("Enter value of c: "); c = sc.nextDouble(); // calculate the value of discriminant b^2 - 4ac d = b * b - 4 * a * c; // if d < 0, the roots are complex // if d = 0, the roots are real and equal // if d > 0, the roots are real and distinct if (d < 0) { System.out.println("The roots are complex."); // calculate real part r1 = (-b) / (2 * a); // calculate imaginary part im = Math.sqrt(d * -1) / (2 * a); // display roots System.out.println("Root 1: " + r1 + " + " + im + "i"); System.out.println("Root 2: " + r1 + " - " + im + "i"); } else if (d == 0) { System.out.println("The roots are real and equal."); // calculate the root r1 = (-b) / (2 * a); // display roots System.out.println("Root 1: " + r1); System.out.println("Root 2: " + r1); } else if (d > 0) { System.out.println("The roots are real and unique."); // calculate the roots r1 = ((-b) + Math.sqrt(b * b - 4 * a * c)) / (2 * a); r2 = ((-b) - Math.sqrt(b * b - 4 * a * c)) / (2 * a); // display roots System.out.println("Root 1: " + r1); System.out.println("Root 2: " + r2); } } }
Output
Case 1:
Quadratic equation ax^2 + bx + c = 0
Enter value of a: 3
Enter value of b: 2
Enter value of c: 4
The roots are complex.
Root 1: -0.3333333333333333 + 1.1055415967851332i
Root 2: -0.3333333333333333 - 1.1055415967851332i
Case 2:
Quadratic equation ax^2 + bx + c = 0
Enter value of a: 4
Enter value of b: -20
Enter value of c: 25
The roots are real and equal.
Root 1: 2.5
Root 2: 2.5
Case 3:
Quadratic equation ax^2 + bx + c = 0
Enter value of a: 9
Enter value of b: -68
Enter value of c: 35
The roots are real and unique.
Root 1: 7.0
Root 2: 0.5555555555555556
4.4. Python Program & output to find the roots of a quadratic equation
#******************************************************** # alphabetacoder.com # Python program to find the roots of quadratic equation #******************************************************** import math # take input of a, b, c # for quadratic equation # ax^2 + bx + c = 0 print("Quadratic equation ax^2 + bx + c = 0") a = float(input("Enter value of a: ")) b = float(input("Enter value of b: ")) c = float(input("Enter value of c: ")) # calculate the value of discriminant b^2 - 4ac d = b * b - 4 * a * c # if d < 0, the roots are complex # if d = 0, the roots are real and equal # if d > 0, the roots are real and distinct if d < 0: print("The roots are complex.") # calculate real part r1 = (-b) / (2 * a) # calculate imaginary part im = math.sqrt(d * -1) / (2 * a) # display roots print("Root 1: ", r1, "+", im, "i") print("Root 2: ", r1, "-", im, "i") elif d == 0: print("The roots are real and equal.") # calculate the root r1 = (-b) / (2 * a) # display roots print("Root 1: ", r1) print("Root 2: ", r1) elif d > 0: print("The roots are real and unique.") # calculate the roots r1 = ((-b) + math.sqrt(b * b - 4 * a * c)) / (2 * a) r2 = ((-b) - math.sqrt(b * b - 4 * a * c)) / (2 * a) # display roots print("Root 1: ", r1) print("Root 2: ", r2)
Output
Case 1:
Quadratic equation ax^2 + bx + c = 0
Enter value of a: 1
Enter value of b: 1
Enter value of c: 1
The roots are complex.
Root 1: -0.5 + 0.8660254037844386 i
Root 2: -0.5 - 0.8660254037844386 i
Case 2:
Quadratic equation ax^2 + bx + c = 0
Enter value of a: 49
Enter value of b: -70
Enter value of c: 25
The roots are real and equal.
Root 1: 0.7142857142857143
Root 2: 0.7142857142857143
Case 3:
Quadratic equation ax^2 + bx + c = 0
Enter value of a: 2
Enter value of b: 20
Enter value of c: -27
The roots are real and unique.
Root 1: 1.2048368229954285
Root 2: -11.204836822995428
4.5. C# Program & output to find the roots of a quadratic equation
/************************************************* alphabetacoder.com C# program to find the roots of quadratic equation **************************************************/ using System; namespace QuadraticEquation { class Program { static void Main(string[] args) { // delclare variables double a, b, c, d, r1, r2, im; // take input of a, b, c // for quadratic equation // ax^2 + bx + c = 0 Console.WriteLine("Quadratic equation ax^2 + bx + c = 0"); Console.Write("Enter value of a: "); a = Convert.ToDouble(Console.ReadLine()); Console.Write("Enter value of b: "); b = Convert.ToDouble(Console.ReadLine()); Console.Write("Enter value of c: "); c = Convert.ToDouble(Console.ReadLine()); // calculate the value of discriminant b^2 - 4ac d = b * b - 4 * a * c; // if d < 0, the roots are complex // if d = 0, the roots are real and equal // if d > 0, the roots are real and distinct if (d < 0) { Console.WriteLine("The roots are complex."); // calculate real part r1 = (-b) / (2 * a); // calculate imaginary part im = Math.Sqrt(d * -1) / (2 * a); // display roots Console.WriteLine("Root 1: " + r1 + " + " + im + "i"); Console.WriteLine("Root 2: " + r1 + " - " + im + "i"); } else if (d == 0) { Console.WriteLine("The roots are real and equal."); // calculate the root r1 = (-b) / (2 * a); // display roots Console.WriteLine("Root 1: " + r1); Console.WriteLine("Root 2: " + r1); } else if (d > 0) { Console.WriteLine("The roots are real and unique."); // calculate the roots r1 = ((-b) + Math.Sqrt(b * b - 4 * a * c)) / (2 * a); r2 = ((-b) - Math.Sqrt(b * b - 4 * a * c)) / (2 * a); // display roots Console.WriteLine("Root 1: " + r1); Console.WriteLine("Root 2: " + r2); } // wait for user to press any key Console.ReadKey(); } } }
Output
Case 1:
Quadratic equation ax^2 + bx + c = 0
Enter value of a: 1
Enter value of b: 1
Enter value of c: 1
The roots are complex.
Root 1: 0.5 + 1.3228756555323i
Root 2: 0.5 - 1.3228756555323i
Case 2:
Quadratic equation ax^2 + bx + c = 0
Enter value of a: 1
Enter value of b: -6
Enter value of c: 9
The roots are real and equal.
Root 1: 3
Root 2: 3
Case 3:
Quadratic equation ax^2 + bx + c = 0
Enter value of a: 1
Enter value of b: 5
Enter value of c: -20
The roots are real and unique.
Root 1: 2.6234753829798
Root 2: -7.6234753829798