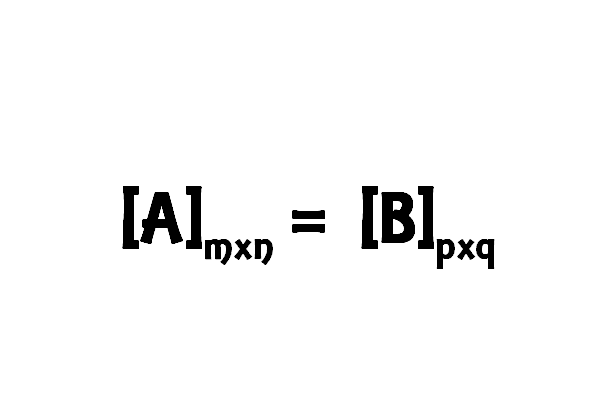Home / Matrix / Python / Python Program to Check The Equality of Two Matrices

Python Program to Check The Equality of Two Matrices

in ,
Check The Equality of Two Matrices

Python program to check the equality of two matrices has been shown here. Two matrices $[A]_{m \times n}$ and $[B]_{p \times q}$ are considered to be equal if both of the following conditions are satisfied

(i) Number of rows and columns are same for both of the matrices i.e. $m = p$ and $n = q$

(ii) Each elements of $A$ is equal to corresponding element of $B$ i.e. $A_{ij} = B_{ij}$ for each $i \in m$ and $j \in n$.






1. Python Program to check the equality of two matrices

Code has been copied
#***************************************
#        Alphabetacoder.com
# Python program to check equality of two matrices
#***************************************

# initialize variable
flag=0
# take input of the order of first matrix
print("Enter the number of row and column of first matrix=")
m, n=map(int, input().split())

# declare first matrix of m x n order with zero initialization
A = [[0 for j in range(n)] for i in range(m)]

print("Enter the first matrix of order ",m," x ",n,"=")
#take input of the elements first matrix
for i in range(m):
    for j in range(n):
        A[i][j]=int(input())

#take input of the order of second matrix
print("Enter the number of row and column of second matrix=")
p, q=map(int, input().split())

# declare second matrix of p x q order with zero initialization
B = [[0 for j in range(q)] for i in range(p)]

#take input of the second matrix
print("Enter the second matrix of order ",p," x ",q,"=");
for i in range(p):
    for j in range(q):
        B[i][j]=int(input())

# check if orders of matrices are same
# if the orders are not same then check each corresponding elements
if m!=p or n!=q:
    print("Matrices are of different order,hence not equal")
    flag=1
else:
    #check equality of each corresponding elements
    for i in range(m):
        for j in range(n):
            if A[i][j]!=B[i][j]:
                #inequal element spotted 
                print("Matrices are not equal. Element mismatch at row ",(i+1)," column ",(j+1))
                flag=1
                break
        if flag==1:
            break
# flag=0 means that each corresponding elements of both matrices are equal and 
# order of matrices are equal
if flag==0:
    print("Matrices are equal")

Output

Case 1:

Enter the number of row and column of first matrix=2 2

Enter the first matrix of order 2 x 2=

1

2

3

3

Enter the number of row and column of second matrix=2 1

Enter the second matrix of order 2 x 1=

1

2


Matrices are of different order,hence not equal


Case 2:

Enter the number of row and column of first matrix=2 2

Enter the first matrix of order 2 x 2=

1

2

3

4

Enter the number of row and column of second matrix=2 2

Enter the second matrix of order 2 x 2=

1

2

3

4

Matrices are equal


Case 3:

Enter the number of row and column of first matrix=1 2

Enter the first matrix of order 1 x 2=

1

5

Enter the number of row and column of second matrix=1 2

Enter the second matrix of order 1 x 2=

1

7


Matrices are not equal. Element mismatch at 1 row 2 column




Labels: ,