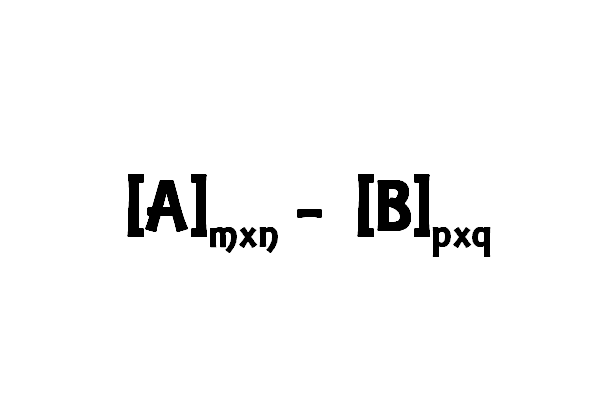Java Program for Matrix Subtraction

Java program to subtract two matrices has been shown here. Two matrices $[A]_{m \times n}$ and $[B]_{p \times q}$ are considered for Subtraction if the number of rows and columns are same in both of the matrices i.e. $m = p$ and $n = q$.

Page content(s):

1. Program & Output: Iterative approach

Additional content(s):

1. Algorithm

2. Pseudocode

3. Time Complexity

1. Java Program for matrix Subtraction

Code has been copied

/***************************************
        alphabetacoder.com
  Java program for Matrix Subtraction
***************************************/

import java.util.Scanner;
public class Subtraction{
    public static void main(String args[]){
        //System.in is a standard input stream
        // sc is the object
        Scanner sc= new Scanner(System.in);
        int m,n,p,q,i,j;
        
        //take input of the order of first matrix
        System.out.print("Enter the number of row and column of first matrix=");
        m=sc.nextInt();
        n=sc.nextInt();
        
        //declare first matrix
        int A[][]=new int[m][n];
        //take input of the first matrix
        System.out.print("Enter the first matrix of order "+m+" x "+n+"=\n");
        for(i=0;i<m;i++)
            for(j=0;j<n;j++)
                A[i][j]=sc.nextInt();

         //take input of the order of second matrix
        System.out.print("Enter the number of row and column of second matrix=");
        p=sc.nextInt();
        q=sc.nextInt();
        
        //declare second matrix
        int B[][]=new int[p][q];
        //take input of the second matrix
        System.out.print("Enter the second matrix of order "+p+" x "+q+"=\n");
        for(i=0;i<p;i++)
            for(j=0;j<q;j++)
                B[i][j]=sc.nextInt();

        // check if order of matrices are same
        // if not then Subtraction of two matrices is not possible
        if(m!=p||n!=q)
            System.out.print("\nMatrices are of different order, hence Subtraction is not possible");
        else{
            //subtract each element of B from corresponding element of A
            // and print the resultant matrix 
            System.out.print("The resultant matrix after Subtraction:\n");
            for(i=0;i<m;i++){
                for(j=0;j<n;j++)
                    System.out.print(" "+(A[i][j]-B[i][j]));
                System.out.print("\n");
            }
        }
    }
}

Output

Case 1:

Enter the number of row and column of first matrix=3 3

Enter the first matrix of order 3 x 3=

3 5 7

4 5 9

0 1 1

Enter the number of row and column of second matrix=3 3

Enter the second matrix of order 3 x 3=

9 4 5

3 7 8

1 2 3

The resultant matrix after Subtraction:=

-6 1 2

1 -2 1

-1 -1 -2

Case 2:

Enter the number of row and column of first matrix=3 3

Enter the first matrix of order 3 x 3=

3 5 7

4 5 9

0 1 1

Enter the number of row and column of second matrix=2 3

Enter the second matrix of order 2 x 3=

9 4 5

3 7 8

Matrices are of different order,hence Subtraction is not possible